Karnaugh Map

Peran Gerbang Logika dan Aljabar Boolean dalam Perkembangan Teknologi

A. Peran Gerbang Logika dan Aljabar Boolean

    Aljabar boolean mempunyai aplikasi yang luas dalam beberapa bidang. Sebagai contohnya, di bidang ketenikan dan jaringan pensaklaran. Satu diantaranya adalah dalam sirkuit elektronik. Sirkuit menerima masukan dan keluaran berupa pulsa-pulsa listrik yang dapat dipandang sebagai 0 dan 1. Aljabar boolean digunakan untuk memodelkan sirkuit elektronik. Elemen dasar dari sirkuit adalah gerbang (gate). Sirkuit elektronik dimodelkan dengan sejumlah gerbang logika (logic gate). Setiap gerbang mengimplementasikan sebuah operasi boolean. Ada tiga macam gerbang dasar yaitu : NOT, AND, dan OR. Sirkuit yang dibentuk oleh kombinasi beberapa gerbang logika disebut sirkuit logika. 

Berikut adalah penjelasan untuk ketiga gerbang tersebut :

    1. Gerbang NOT. Sebuah gerbang NOT adalah gerbang dengan satu sinyal input dan satu sinyal output, dan keadaan outputnya selalu merupakan kebalikan dari keadaan inputnya, sehingga outputnya sering dinamakan sebagai komplemen dari inputnya. Dalam aljabar boolean gerbang NOT dapat dinyatakan dalam persamaan boolean (yang variabelnya bernilai 0 atau 1) yaitu : y = NOT a atau y = a Jika a bernilai 0 maka y = NOT 0 = 1 atau y = a = 0 = 1, dan jika a bernilai 1 maka y = NOT 1 = 0 atau y = a = 1 = 0. Berikut tabel kebenaran untuk gerbang NOT : 

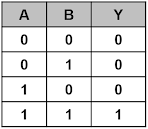
    2. Gerbang AND. Gerbang AND mempunyai dua atau lebih input tetapi hanya satu output. Untuk mendapatkan output yang bernilai 1 maka semua inputnya harus bernilai 1, selainnya outputnya akan 0. Dalam aljabar boolean gerbang AND dapat dinyatakan dalam persamaan boolean sebagai berikut :

    y = a AND b atau y = a . b atau y = a b 

Berikut tabel kebenaran untuk gerbang AND : 

    3. Gerbang OR. Gerbang OR mempunyai dua atau lebih sinyal input tetapi hanya satu sinyal output, jika terdapat nilai input 1 maka output yang dihasilkan adalah 1. Dalam aljabar boolean gerbang OR dapat dinyatakan dalam persamaan boolean sebagai berikut : y = a OR b atau y = a + b 

Berikut tabel kebenaran untuk gerbang OR : 

    Sebagai ilustrasi pembahasan disain kontrol gerbang lintas kereta api, akan dimisalkan terdapat tiga buah input dan dua buah sensor yang berfungsi untuk membuka dan menutup gerbang, serta timer sebagai penunjuk waktu yang akan menunjukkan kondisi on pada saat gerbang descending untuk posisi gerbang tertutup, atau gerbang ascending untuk posisi gerbang terbuka. Saat suatu kereta memasuki area gerbang, maka sensor U1 mulai bekerja untuk menutup gerbang dan juga timer U3 mulai bekerja hingga gerbang benar-benar dalam posisi tertutup. Gerbang tetap tertutup hingga kereta tersebut meninggalkan area gerbang dan pada saat yang bersesuaian sensor gerbang U2 mulai bekerja untuk membuka gerbang dan timer mulai bekerja untuk proses membuka gerbang. Jika terdapat kereta lain yang memasuki area gerbang pada posisi gerbang sedang terbuka, maka dengan segera gerbang akan tertutup. 

    Fundamental sistem kerjanya ditunjukan melalui gambar 1. Desain sistem tersebut terdiri atas empat state (keadaan), yaitu : S1 (gerbang di atas), S2 (gerbang di bawah), S3 (gerbang menuju bawah), dan S4 (gerbang menuju atas). Transisi antar state-state tersebut akan diatur  oleh sensor input U1 , U2 , dan U3 . Sensor U1 bernilai true for close, sensor U2 bernilai true for open, dan sensor U3 bernilai true for timer on and false for timer of. 

    Terhadap disain sistem tersebut, dilakukan spesifikasi dan verifikasi dua sifat, yaitu safety dan functionality. Sifat safety : gerbang sedang tertutup atau gerbang tertutup dan kereta berada disekitar area gerbang 

(NOT U1 AND (S1 OR S4)) OR (U1 AND U3 AND S3) OR (U1 AND NOT U3 AND S2)  

Sifat functionality : gerbang terbuka saat kereta tidak berada disekitar area gerbang  

  (NOT U2 AND (S2 OR S3)) OR (U2 AND (S1 OR S4)) 

Penutup Kereta api merupakan alat transportasi dengan daya angkut besar dan melayani perjalanan dengan jarak tempuh relatif jauh. Jalan kereta api merupakan jalan khusus berupa rel, yang dibangun khusus hanya dipergunakan oleh kereta api, sehingga dapat dikatakan bahwa rel adalah jalan bebas hambatan. Bahkan pada sejumlah tempat perpotongan dengan jalan raya, jalan kereta api diistimewakan, jalan raya ditutup untuk sementara waktu dan kereta api memperoleh prioritas lewat lebih dahulu. Pengaturannya dapat dilakukan dengan membuat gerbang lintas kereta api, yang bagian desainnya dapat dilakukan dengan menggunakan operasioperasi aljabar boolean.

Dari penjelasan di atas bisa diketahui bahwa gerbang logika mempunyai banyak peran dalam kehidupan manusia. Terutama dalam bidan teknik.

2. Cara Penyederhanaan Persamaan Logika

    1. Aljabar Boolean

        

        Aljabar Boolean dapat digunakan untuk menganalisa suatu rangkaian logika dan mengekspresikan operasinya secara matematik. Suatu rangkaian dapat direduksi menjadi bentuk yang lebih sederhana dengan menggunakan teorema Boolean tertentu. Ekspresi Boolean yang lebih sederhana ini dapat menggantikan ekspresi aslinya, karena nilainya yang ekivalen. Contohnya : rangkaian dengan persamaan logika
   dapat disederhanakan menjadi , dengan menggunakan teorema-teorema Boolean. Di dalam teorema tersebut, variabel dapat bernilai 0 atau 1.Dibawah ini akan dijelaskan teorema-teorema tersebut, yaitu :
• Teorema 1
Setiap variabel apabila di AND kan dengan 0, hasilnya harus sama dengan 0. Hal itu sesuai dengan table kebenaran dari gerbang AND, yaitu apabila salah satu input bernilai 0, maka output akan menjadi 0.
X • 0 = 0
• Teorema 2
Setiap variabel apabila di AND kan dengan 1,maka hasilnya adalah variabel tersebut.
X • 1 = X
• Teorema 3
Dapat dibuktikan dengan mencoba tiap-tiap kasus.Apabila x = 0, maka 0∙0 = 0; apabila x = 1, maka 1∙1 = 1
X • X = X
• Teorema 4
Apabila  suatu variabel di AND kan dengan inverse variabel tersebut, maka hasilnya 0
       X • X’ = 0
• Teorema 5
Apabila 0 di OR kan dengan variabel dengan nilai apapun, maka hasilnya adalah variabel tersebut.
X + 0 = X
• Teorema 6
Apabila suatu variabel di OR kan dengan 1, maka hasilnya akan selalu 1. Kita dapat mengingat bahwa output gerbang OR akan sama dengan 1 apabila salah satu input bernilai 1, tanpa memandeng harga input yang lain. 
X + 1 = 1
• Teorema 7
Dapat dibuktikan dengan memeriksa untuk kedua harga x. 0 + 0 = 0 dan 1 + 1 = 1.
X + X = X
• Teorema 8
Apabila suatu variabel di OR kan dengan inverse variabel tersebut, maka nilainya 1
X + X’ = 1
Variabel X pada teorema 1 sampai dengan 8 dapat menyatakan suatu ekspresi yang mengandung lebih dari satu variable.

Teorema Multivariabel
• Teorema 9 : X + Y = Y + X
• Teorema 10 : X • Y = Y • X
Teorema 9 dan 10 disebut hukum-hukum komutatif. Hukum ini menunjukkan bahwa urutan dalam menjumlah atau mengalikan dua variable tidak penting, karena hasilnya akan sama.

• Teorema 11 : X + (Y + Z) = (X + Y) + Z = X + Y + Z
• Teorema 12 : X (YZ) = (XY) Z = XYZ
Teorema 11 dan 12 disebut hukum-hukum asosiatif, yang menyatakan bahwa kita dapat mengelompokkan term-term dari suatu penjumlahan atau suatu perkalian secara bebas, karena hasilnya akan sama.

• Teorema 13 : X(Y + Z) = XY + XZ
• Teorema 14 : (W + X)(Y + Z) = WY + XY + WZ + XZ
Teorema 13 dan 14 disebut hukum distributif, yang menyatakan bahwa suatu ekspresi dapat dijabarkan dengan mengalikan term demi term persis sama seperti dalam aljabar biasa.

• Teorema 15 : X + X’Y = X + Y (sifat absorpsi)
• Teorema 16 : X + XY = X (sifat reduksi)
Teorema ini dapat dibuktikan dengan menggunakan teorema 6 dan 2 :
X + XY = X(1 + Y)
  = X • 1   (memakai teorema 6)
  = X         (memakai teorema 2)
• Teorema 17 :
▪ Teorema 18 :
• Teorema 19 : AB + AC + BC’ = AC + BC’
• Teorema 20 : (A+B)(A+C)(B+C) = (A+C) (B+C)

    2. Diagram Venn

           Salah satu cara untuk memudahkan untuk melukiskan hubungan antara variabel dalam aljabar boolean adalah dengan  menggunakan diagram venn. Diagram ini terdiri dari sebuah segi empat yang didalamnya dilukis lingkaran-lingkaran yang mewakili variabelnya, satu lingkaran untuk setiap variabelnya. Masing-masing lingkaran itu diberi nama menurut variabel yang diwakilinya. Ditentukan bahwa semua titik diluar lingkaran itu tidak dimiliki oleh variabel tersebut. Misalnya lingkaran dengan nama A, jika dalam lingkaran itu dikatakan bernilai 1, maka diluar a dikatakan bernilai 0. untuk dua lingkaran yang bertumpang tindih, terdapat empat daerah dalam segiempat tersebut.Diagram venn hanya cocok apabila jumlah variabelnya tidak lebih dari 3, karena bila lebih dari 3 variabel akan sulit menghitungnya.

    3. Diagram Venn 

        - 2 variael

        - dan 3 variabel

            Dalam lingkaran itu tampak tiga lingkaran yang bertumpang tindih, satu untuk masing-masing variable A, B dan C. dengan demikian dimungkinkan untuk membedakan delapan daerah yang terpisah dalam diagram venn dengan variable itu. Dalam hal ini hukum distributif dibuktikan dengan menunjukan bahwa daerah yang memotong lingkaran A dengan daerah yang meliputi B atau C adalah daerah yang sama yang dimiliki oleh AB atau A.

3. Bentuk Kakonik

    PENGERTIAN

       Bentuk Kanonik merupakan Fungsi Boolean yang diekspresikan dalam bentuk SOP (Sum of Product) atau POS (Product of Sum) dengan minterm/maxterm. Kanonik memiliki literal yang lengkap. Sedangkan bentuk baku merupakan Fungsi Boolean yang diekspresikan dalam bentuk SOP atau POS dengan minterm atau maxterm mempunyai literal yang tidak lengkap.  Untuk dalam memahami secara lengkap SOP (Sum of Product) diistilahkan dengan jumlah dari hasil perkalian. POS (Product of Sum) diistilahkan dengan perkalian dari hasil penjumlahan.

Untuk dapat memperoleh ekspresi Boolean yang harus diperhatikan hanyalah “output = 1”.  Suku-suku bentuk SOP disebut minterm. sedangkan Untuk mendapatkan mendapatkan bentuk POS (maxterm) diperhatikan hanyalah “keluaran bernilai 0”.

TABEL BOOLEAN BENTUK IKONIK DAN BAKU

Tabel kebenaran adalah tabel yang memuat semua kemungkinan atau kombinasi masukan serta keluaran dari kombinasi tersebut. pada umumnya tabel kebenaran yang memiliki nilai “n” masukan mempunyai “2n”. untuk dapat memahami table tersebut, berikut table kebenaran :

Contoh 1 :

Membuat ekspresi Boolean dalam bentuk SOP dan POS dari tabel kebenaran ini :

Penyelesaian :

a. Dalam bentuk SOP, maka yang dilihat adalah Y = 1

b. Dalam bentuk POS, maka yang dilihat adalah Y = 0

            Contoh 2 :

Dalam suatu BANK terdapat beberapa Brangkas yang berisi uang, emas, dan dokumen-dokumen penting lainnya. dalam BANK tersebut terdapat beberapa direktur dan direktu. untuk dapat membuka brangkas tersebut minimal 2 orang baik direksi maupun direktur untuk dapat membuka bangkas tearsebut.   Dalam kasus tersebut, buatlah rangkaian logika sederhana agar case tersebut bisa berjalan :

Penyelesaian :

Dari soal menunjukkan bahwa lemari akan terbuka jika minimal 2 orang dari 3 orang yang ada (dapat menggunakan SOP).a) Masukan (nilai “0” berarti tidak ada orang sedang nilai “1” berarti ada orang).b) Keluaran (nilai “0” berarti pintu tertutup sedang nilai “1” berarti pintu terbuka).

Tabel Kebenarannya :

Gambar rangkaian logikanya: